The third part of this series presented PBKDF2 as a modern key derivation and password hashing algorithm. But PBKDF2 has its limitations; for best protection against password cracking the iteration count (defining the computing power needed to hash a password) should be chosen as high as possible. On the other hand, a higher iteration count also means that a login of a regular user will be slower. The maximal time users are prepared to wait for a successfull login will limit the maximal iteration count which you can choose for the available computing power.
For some time we could at least assume that all but the most resourcefull attackers will have roughly the same computing power at hand as the defenders have on their login servers. An attacker might be able to set up (and finance) hardware to hash passwords 100 or even 1000 times faster than a server, but this could be compensated for by a sufficiently high iteration count. However, by using hardware specialized towards massively parallel execution of hashing operations the relation of the average servers and the potential attackers “hashing power” shifted more and more to the advantage of the attacker. Hashing algorithms like the scrypt algorithm presented in this Blog article attempt to shift this relation back in favor of the defender.
Hardware Supported Attacks
The key to a successfull attack on password hashing algorithms like PBKDF2 is parallelization. A salted password hash is cracked by hashing a dictionary of potential passwords using the same algorithm and salt, and comparing the results against the given password hash. The expensive operation here is the hashing, while the mere comparison of the hashes even for very big dictionaries can be done quickly with any modern database even on moderate hardware.
The salt (see part 2) prevents the attacker from precomputing all the password hashes of the dictionary and use these one-time precomputed values for all password hashes to be cracked. Thanks to the salt each password hash is “unique” and the attacker is forced to to recalculate the dictionary hashes for each specific target hash.
However, the process of computing password hashes can be highly parallelized by splitting the dictionary test potential passwords in parallel. If you had a dictionary of one million possible passwords and hardware which can do one million of password hashing operations concurrently, you can check your complete dictionary against a given password hash in roughly the time needed to do a single-threaded password hash calculation. Even if your single-threaded hashing performance is very low compared to the attacked servers performance, the check of the complete dictionary will be rather fast.
The first blow to algorithms like PBKDF2 came with the use of GPUs as general purpose computing devices which allowed highly parallel calculations not comparable with the use of conventional CPUs. But nowadays hashing is done even more efficiently by Application Specific Integrated Circuits (“ASICs”) which are specifically customized to attack a specific hashing algorithm.
The drive to extremely parallelize hashing did not come from password crackers but rather from the “mining” of cryptocurrencies, first and foremost Bitcoin mining. Mining Bitcoins or other cryptocurrencies in essence boils down to do hash calculations faster than your competitors. Because miners can make real money with their activity, they are willing to invest into specialized hardware to gain an advantage above the competitors. (And if the competitors don’t want to fall out of the race, they will be forced to follow suit.) This flow of money into companies and factories producing ASICs for cryptocurrency mining pushed the further development of these systems.
As a mere side effect of the cryptocurrency mining game, attackers of password hashes will have comparatively cheap but very powerfull ASIC hardware easily available, which with some customization will allow to calculate password hashes in an order of magnitudes faster than any conventional server. Against an attacker employing such hardware the PBKDF2 algorithm will be a rather weak defense.
scrypt to the Defense
Searching for a way to defend password hashes against highly parallel attacks it is helpfull to realize that highly parallel systems have an inherent memory problem. If you have a real lot of parallel threads and each thread needs a real lot of memory, then you will need a real whopping lot of memory driving your hardware costs considerably higher.
So what we are looking for is an algorithm which not only lets us tweak the computing power requirement (like PBKDF2) but also lets us enforce the use of a certain amount of memory to compute a password hash. On a regular PC or server you will have at most a few threads doing user logins concurrently (each doing a single-threaded password hash operation) and there will be plenty of memory for every thread. A highly-parallel ASIC system on the other hand, will have much more limited memory resources per thread due to the high number of concurrent threads. (You may invest more of the available transistors to memory but this will leave less for the processing and considerably decrease the number of concurrent threads possible.)
As of today, the best known “memory hard” password hashing algorithm is the scrypt algorithm. In this article I will focus on the scrypt algorithm as it is being currently standardized in the RFC draft draft-josefsson-scrypt-kdf-01 (“The scrypt Password-Based Key Derivation Function”). The original paper presenting the algorithm can be found here: https://www.tarsnap.com/scrypt/scrypt.pdf (PDF)
Let’s start with a birds eye view of the algorithm:
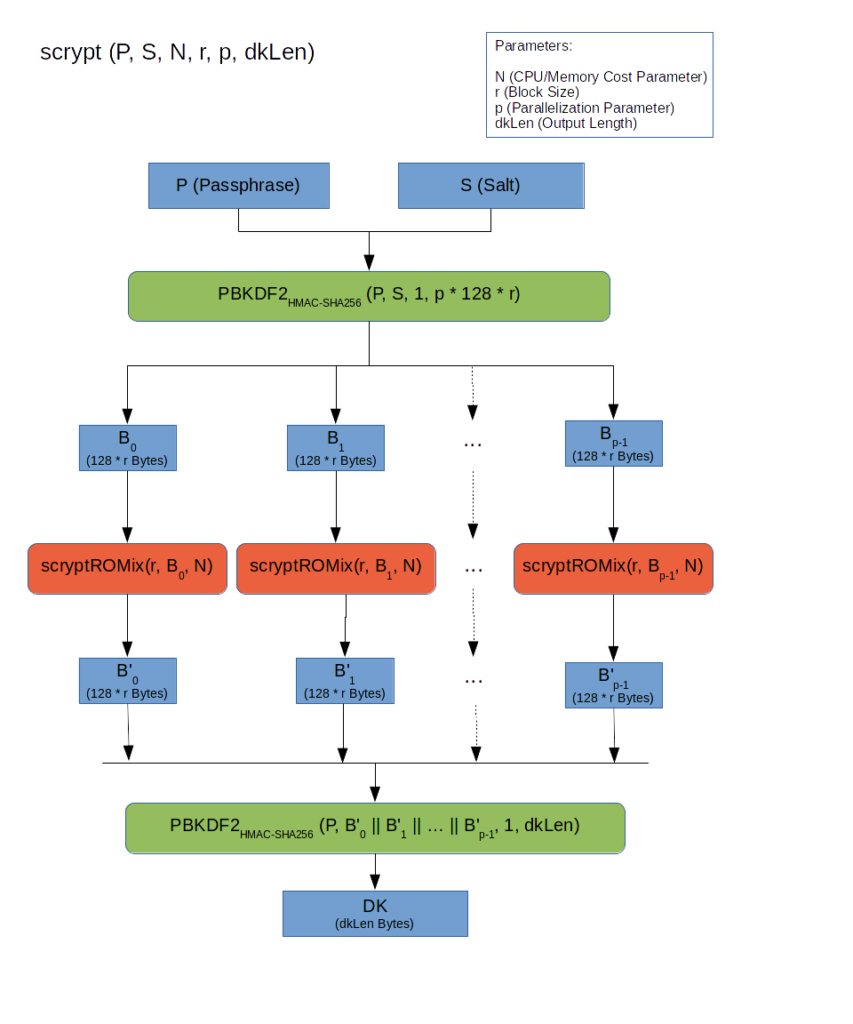
The basic input to the algorithm is the passphrase and the salt which we already know well from the previous parts of this article series. In addition the algorithm can be configured using several parameters:
- CPU/Memory Cost Parameter (N): As we will see, this is the equivalent to the iteration count in PBKDF2 and determines how much processing time and/or memory is needed to execute the algorithm. As with an iteration count you want to choose this parameter as high as possible to make the attackers life harder.
- Block Size (r): The block size determines the memory needed for a basic block processed by the core part of the algorithm, the scryptROMix function. By increasing the block size you increase the memory requirements without considerably influencing the CPU requirements.
- Parallelization Parameter (p): As you can see in the overview above, the algorithm splits the work into p scryptROMix operations which can be executed concurrently. The parallelization parameter allows to finetune the “concurrency” of the algorithm and increase the CPU requirements without increasing the memory requirements.
- Output Length (dkLen): This is simply the number of bytes finally produced by the algorithm. For our use case of password hashing you will normally choose a value around 32 bytes (or 256 bits) for a reasonable hash size. (In other use cases, namely the generation of key material, you would choose the output length according to the number and sizes of the key(s) being generated.) The output length is only relevant for the last PBKDF2 operation and does not otherwise influence the algorithm.
The basic structure of the scrypt algorithm as presented in the overview diagram above is not very impressing. First PBKDF2 is used to mix the input data and “stretch” or “trim” it to the input size neded by the core of the scrypt algorithm. The result of the PBKDF2 operation is a “homogeneous” byte string which can be split into p blocks, each containing r bytes. (Note that the iteration count chosen for the PBKDF2 function is 1 since we don’t use PBKDF2 here to maximize processing time.)
The blocks are then processed independently from each other by the scryptROMix operation (which will be explained below). This block processing can be done concurrently so the number of blocks (p) determines the “maximal concurrency” of the algorithm.
Finally the result of each scryptROMix operation is once again mixed and “stretched” or “trimmed” to the desired output size (dkLen), using PBKDF2 with an iteration count of 1 as before.
The algorithm overview looks quite reasonable but does not give us any insight into the specific qualities of scrypt. While we see that we can tweak the “concurrency” by modifying the parameter p, the meaning of the other parameters and how the influence the processing power and memory requirements is still a mystery.
The solution to the mystery lies in the scryptROMix operation:
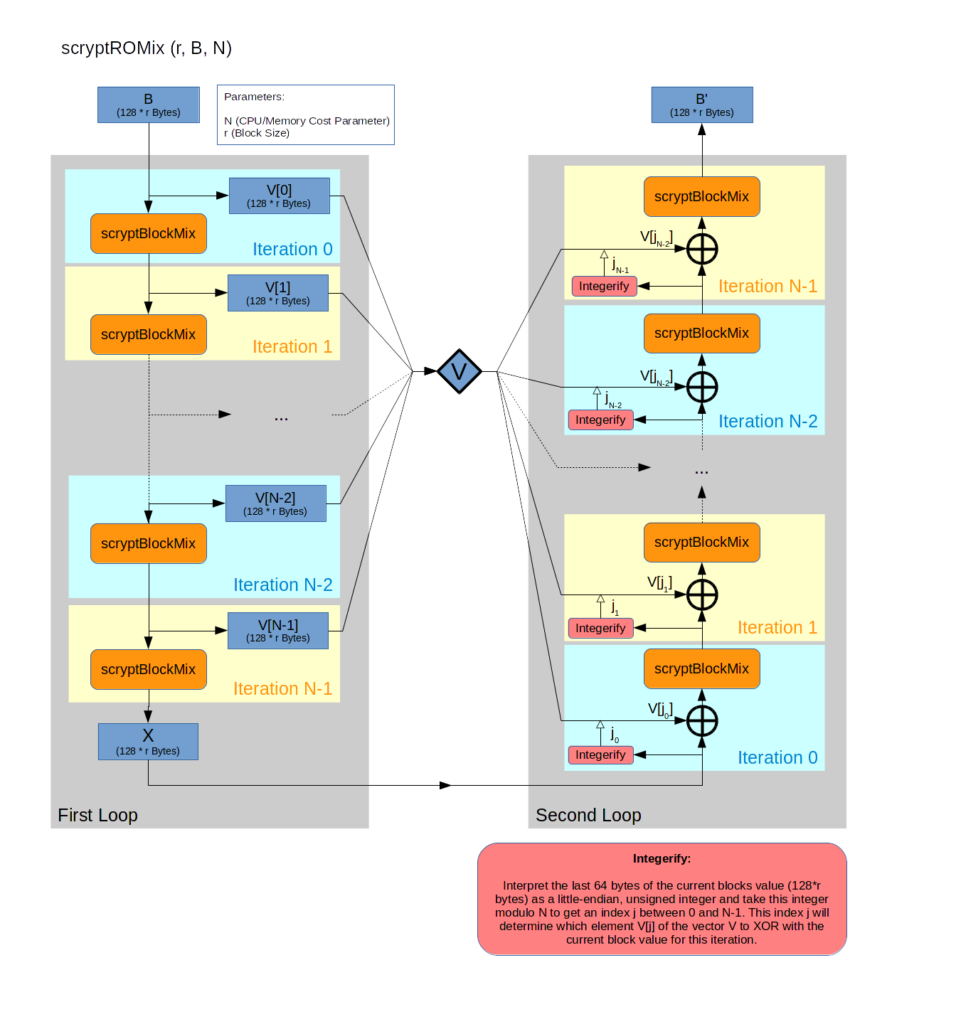
The scryptROMix operation essentially consists of a sequence of scryptBlockMix operations on the input block of 128 * r bytes. We will have a more detailed look at scryptBlockMix below, but its essential property is to mix all bits of the input block in some “unpredictable” way and producing an output block of equal size to the input block.
The scryptBlockMix sequence itself is split into two “loops” with N iterations per loop. In the first loop a vector V consisting of the N input blocks of each iteration is stored.
A single block of the vector V is then xored into the input block of each scryptBlockMix operation of the second loop. Note that the last bytes of the input block itself determine which block of V to choose for the specific iteration.
Compared to the scryptROMix operation, scryptBlockMix is rather simple again:
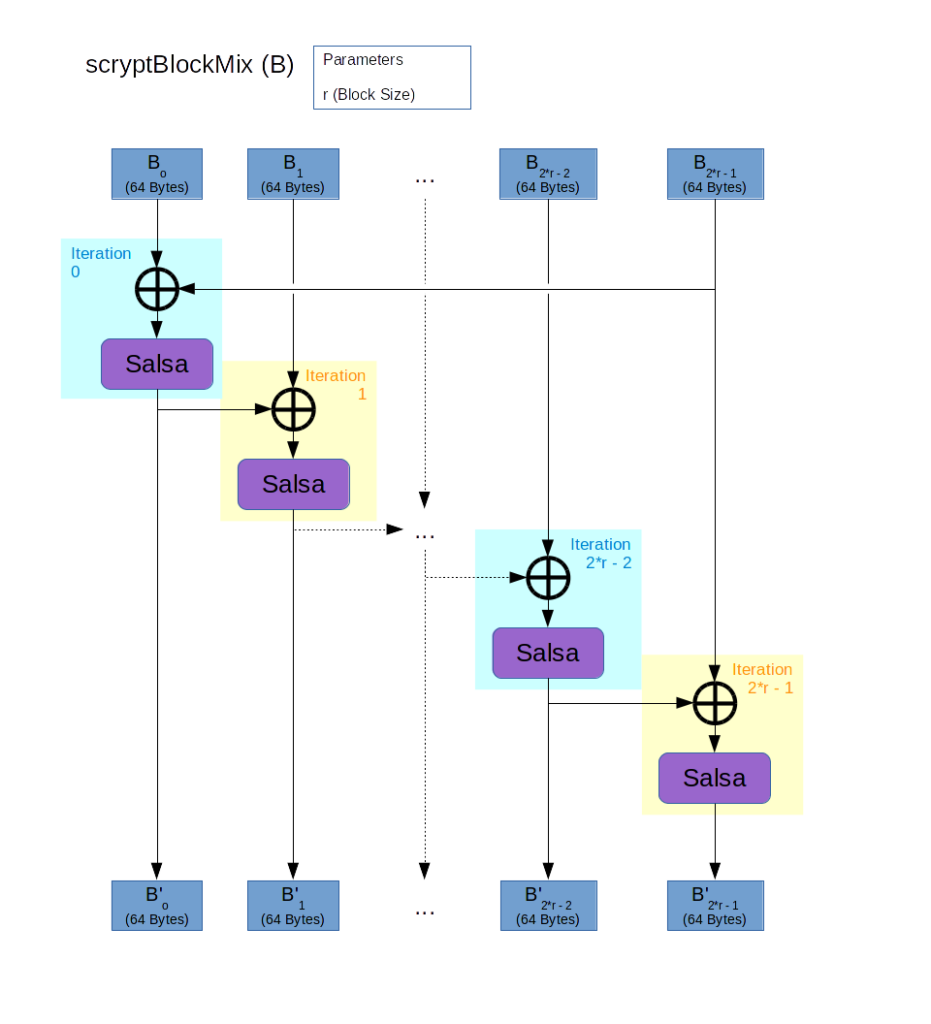
Here the Salsa operation stands for the Salsa20/8 Core algorithm which is a variant of Salsa20 Core reduced from 20 to 8 rounds. The Salsa20 Core algorith is a function which mixes the input bits similar to a hash function but works on strings of 64 bytes and produces output of the same size.
Salsa20 Core has been designed for the Salsa20 encryption function, but scrypt does not otherwise have anything to do with Salsa20. In fact, the original paper presenting scrypt (Stronger Key Derivation Via Sequential Memory-Hard Functions) does not specifically request Salsa20/8 Core but states that Salsa20/8 Core seems to be an ideal match for scrypt because it is fast but not parallelizable, which are both properties desirable for the mix function used in scrypt.
Note that Salsa20 Core does not have the properties of a cryptographical hash function. This is not necessary for the application in scrypt which works with any mix function (where each output bit depends on each input bit) which is fast, not parallelizable and not “predictable” in a sense that there is a more efficient way to determine the output for a given input than actually executing the calculations of the algorithm. (Since the number of possible input strings is finite it would theoretically be possible to build a complete table of inputs and outputs, but the huge number of input strings makes this infeasible in practice.)
scryptBlockMix then just splits its input into blocks of 64 bytes size and applies the Salsa20/8 Core function to the blocks to produce the corresponding output block. To intermix all bits of each block with all the bits of each other block, the first input block is xored with the last input block and each other input block is xored with the previous output block.
This essentially “stretches” the Salsa20/8 Core function from the fixed block size of 64 bytes to the variable block size of the blocks processed by the scryptROMix operation. Note that the basic properties of the Salsa20/8 Core function are retained: The value of each output bit depends on the value of each input bit and the process is not (significantly) parallelizable. (Since the input of each Salsa calculation depends on the output of the previous Salsa calculation, these calculations cannot be done concurrently.)
How it Works
So how does scrypt enforce minimal memory requirements? The answer lies in the vector V of the scryptROMix algorithm. This vector of 128 * r * N bytes is built in the first loop of the algorithm and by choosing essentially unpredictable elements from that vector in the second loop the engine executing the algorithm will be forced to keep the complete vector readily available in memory (ideally in the CPU cache) to maximize execution speed.
As you will notice, it is not really necessary to keep the complete vector in memory to execute the algorithm. As it turns out it is really difficult to “force” an algorithm engine to use a considerable amount of memory for the execution of an algorithm like scrypt. In practice there will always be the possibility trade memory against processing power. One could easily implement scryptROMix without storing the vector V at all! When accessing a specific element of V in the second loop the calculations of the first loop can be repeated up to the iteration corresponding to the requested element, therefore “recalculating” that vector element. By storing a variable number of intermediate results of the first loop (instead of each result) an attacker might even finetune the CPU/memory tradeoff to best suit his means.
However, the crucial point is that doing such recalculations instead of storing the vector will increase the necessary processing power by such factors that the advantage of highly parallel hardware is compensated. At least that is the promise of scrypt.
But we have not seen the end of the evolution yet. After the success of Bitcoin a great number competing crypto currencies (more than 275 by May 2014 according to Wikipedia) have sprung up, some of them, like Dogecoin and Auroracoin, using scrypt as their hash algorithm to increase the mining difficulty. As soon as such a crypto currency gains some popularity (which seems to be the case at least for Dogecoin) there will be an increasing incentive to develop hardware specialized into scrypt calculations.
So scrypt is just the next step in the arms race between cryptography and cryptoanalysis, and in my opinion it does not look too good for the defenders. However, if you have a chance to choose scrypt over (say) PBKDF2, you should certainly do so. It may not completely stop every dedicated attacker but it will certainly slow him down and make his job much more difficult and expensive.
Some Practical Advice
When using scrypt you will have to choose the parameters N, r and p. Ideally you would tune these to optimal values according to the amount of memory, parallelism and processing power available at production time and to the properties of the memory subsystem in question.
In practice, needing a quick solution to hash some passwords, you will probably not have the luxury of extensive testing and finetuning. The authors of the scrypt paper recommend r = 8 and p = 1 for typical current PC hardware.
Given the above starting points for r and p you could then try a value around 32’000 for N, which will consume around 16 MiB to store the vector V. If the resulting key derivations are intolerably slow, decrease N possibly while increasing r to keep the memory use constant. On the other hand, if you have some CPU power left, increase either N (which will also increase the memory use) or p (which will increase CPU use without influencing the memory use).
On servers doing a lot of parallel logins, using 16 MiB (or more) per login might be too much. In this case decrease N which will decrease the needed memory as well as the needed processing power. Then increase p as much as tolerable to get the optimal processing power consumption for the chosen N. (An example for a reasonable setup would be N around 1000 and p = r = 8.)
Conclusion
This article ends the password hashing series. I hope I could give you some insight into the importance of hashing password for persistent storage and the inner workings of modern password algorithms.
References
All articles of the series:
- The Importance of Hashing Passwords, Part 1: Cryptographic Hashes: An introduction into cryptographic one-way hashes such as SHA.
- The Importance of Hashing Passwords, Part 2: Spice it up: What is salt and why is it important?
- The Importance of Hashing Passwords, Part 3: Raise the Price: How PBKDF2 attempts to slow down attackers by chaining iterated hash operations.
- The Importance of Hashing Passwords, Part 4: The Hardware Threat: How to use scrypt to defend against dedicated cracking hardware by enforcing minimal memory requirements.
References:
- Finding Preimages in Full MD5 Faster Than Exhaustive Search (Yu Sasaki, Kazumaro Aoki)
- Construction of the Initial Structure for Preimage Attack of MD5 (Ming Mao, Shaohui Chen, Jin Xu)
- Schneier on Security: SHA-1 Broken (Bruce Schneier)
- Cryptography Engineering (Bruce Schneier)
- SplashData News: Worst Passwords of 2012 — and How to Fix Them
- RFC 2104: HMAC: Keyed-Hashing for Message Authentication
- RFC 2898: PKCS #5: Password-Based Cryptography Specification Version 2.0
- Internet Draft: The scrypt Password-Based Key Derivation Function, draft-josefsson-scrypt-kdf-00 (S. Josefsson e.a.)
- The Salsa20 core (D. J. Bernstein)
- Snuffle 2005: the Salsa20 encryption function (D. J. Bernstein)
- Stronger Key Derivation via Sequential Memory-hard Functions [PDF] (Colin Percival)
- Bitcoin Homepage
- Dogecoin Homepage
- Auroracoin Homepage
Wikipedia Glossary:
- Application-specific Integrated Circuit (ASIC)
- Birthday Attack
- Bitcoin
- Bitcoin Mining
- Cryptocurrency
- Cryptographic Hash Function
- General-purpose Computing on Graphics Processing Units
- HMAC
- Key Derivation Function
- Length Extension Attack
- MD5
- Message Authentication Code
- PBKDF2
- Rainbow Table
- RIPEMD-160
- Salt (Cryptography)
- scrypt
- SHA-1
- SHA-2
- SHA-3
