The last part of this series presented a fairly serious password hashing algorithm using an HMAC and a salt value. However, as this article will show, this construction can be much improved, dramatically raising the “price” for an attacker to crack a password hash.
How to Attack a Password Database
To improve our salted HMAC construction, we need to know how an adversary will actually attack a hashed password. We will not go into all details of password hash cracking here. For example the question of how to compile an optimal “dictionary” of trial passwords (or if to use brute force instead) is not relevant for our goal to improve the hashing algorithm. But be assured that the contemporary password crackers are very skilled in this area, so even seemingly “excellent” passwords get cracked much faster than possible by a brute-force attack, even though such passwords obey all the rules of using digits and special characters, scrambling words, appending pseudo-random prefixes and suffixes, having a reasonable length and so on.
Assuming that there is no fault in our cryptography (such as a weakness in the applied hash algorithm) and no bug in our implementation, the attacker will have to resort to simply hash many possible passwords and see if the result matches the password hash value at hand. Once a match is found, the corresponding password is cracked.
As seen in the last part, an unsalted password hash offers the possibility to greatly speed up the cracking. If an attacker gets hold of a whole database of hashed passwords (an alarmingly common case) and is interested in the passwords of any users (as opposed to targeting a specific user), he can do a single hashing operation on a trial password and then check against each users hash value. Because the checks are extremely cheap compared to the hashing, this speeds up the cracking of a password almost by the number of users in the database.
However, by salting every password hash with a random value we prevent such an “optimization”. The attacker is now forced to do one hash calculation per password hash for each trial password because the salt makes each password hash unique even if the hashed password is the same.
The crucial observation here is that the attacker will need to do a very high number of password hashing operations to be successfull. While the exact number of operations needed depends on the strength of the passwords in relation to the dictionary of trial passwords (and possibly some luck), the time needed to execute these operations directly depends on the average time needed to execute a hashing operation. (Note that there is some other work to be done such as generating the trial passwords, checking for matches etc. But compared to the actual hashing operation this additional “housekeeping” is usually negligible.)
Now it is not to difficult to see that by making the hashing operations even more “expensive” we can further slow down an attacker. But as software developers we are usually conditioned to “optimize” our algorithm, so doing the opposite is somewhat counter-intuitive. Won’t that hurt the performance of our system? Well, as it turns out, in many cases not so much. We normally need to check the password when a user logs into a system, which often happens a few times per day or even much less frequently. In many situations it will be completely tolerable if a password hashing operation needs a few seconds, because the users can accept to wait a moment for the login process to complete and logins happen infrequently enough that processing power on the server is not an issue. (In a sessionless setup, for example with HTTP basic authentication, when you need to re-authenticate for every request you will probably want to reconsider your options. For the reminder of the article we will assume a “session based” login, where the conditions to make a “slow” password hashing acceptable are fulfilled.)
So a password hashing algorithm which takes a second or two on our average server should be fine for us. Compare this with the situation of the attacker: Using a modern PC with a high grade GPU it is easily possible to do 1 billion HMAC calculations per second on the GPU. That amounts to a really big number of trial passwords which can be tested in a very short time. But let’s assume we can make a single hash calculation 10 million times more expensive. In this case the attacker will be reduced to 100 tests per second which (from our point of view) is a huge improvement.
What is the impact on our users? Well, assuming that the server (which does the hash calculations on the CPU instead of the GPU) is about 200 times slower than the attackers GPU when calculating password hashes, we can do a password check on the server in about two seconds. If it is acceptable for your users to wait for these two seconds upon login, you can considerably slow down the attack on the database.
Take Your Time
So how do we make our HMAC hash algorithm from part two more expensive? The core idea is to repeat the hash operation many times. We always take the output of the preceding iteration as input of the following one. The output of the last hash operation is the final password hash.
We could, for example, “chain” the SHA-256 algorithm c times and use this SHAc-256 construction instead of the plain SHA-256 algorithm:
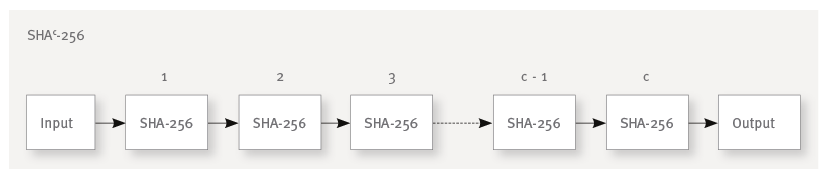
By choosing c we can finetune the tradeoff between additional security and login performance. The goal is to find a value for c which slows down the password hashing process as much as possible without impeding the users login too much. As everyone knows the average computing power will increase with time, so it will pay off to allow future adaption of c (for example when the server application moves to new, faster hardware).
To determine c the machine generating the hash when the user sets his password (which is typically the same verifying passwords against stored hashes later on) might execute (and count) chained hash operations until a certain amount of time (say 1 or 2 seconds) have elapsed. The assumption here is, that the later verification upon login will have a comparable delay.
However, most implementations of standardized “chained” password hashing algorithms (like the PBKDF2 presented below) will not easily allow such sophisticated dynamic determination of the iteration count. For a simplified implementation one could just execute some experimental password hash calculations with different iteration counts on hardware comparable to the intended target machines of the final product. The ideal iteration count determined experimentally can then be specified as some configuration property or even as a compile time constant in the code. From time to time, usually when the performance of the target machines increases, one would repeat the password hashing experiment and determine a new ideal iteration count.
To verify a password from a login attempt against the stored password hash, we will execute the password hashing algorithm with the password to verify and the same salt and iteration count used to generate the stored hash. A stored password entry will therefore now consists of three parts: The actual password hash (i.e. the result of our password hash function), the salt and the iteration count c used to generate the hash.
Note that you cannot “rehash” the stored password hashes (because you don’t know the original password anymore), so even if you configure a fixed iteration count you will have to store the specific iteration count of each password hash and reuse it when verifying a password against that hash. Otherwise increasing the fixed iteration count later on for newly generated password hashes would “invalidate” all previously stored password hashes which is typically not what you want.
PBKDF2
This “hash-chaining” is a very simple way to increase the time needed for hashing … maybe too simple. Many mathematical functions exhibit the property that their results converge to some limit if they are repeatedly applied to their own output. A very obious example is the function f(x) = x / 2 which when repeatedly applied will quickly converge to 0 for every arbitrary start value.
A perfect secure hash algorithm (as explained in the first part of this series) would never exhibit such a convergence. However, while it seems that hash algorithms like the SHA-2 family do a good job, we can be absolutely sure that they are not perfect. As a matter of fact, today no one knows if an algorithm like SHAc-256 might converge for some (or even all) start values if c gets big enough. But an effective protection against such unknown convergences is to mix the original input value into the input of every iteration. This is exactly what PBKDF2 does.
PBKDF2 stands for “Password Based Key Derivation Function, Version 2” and has been standardized in PKCS #5 and RFC 2898. While PBKDF2 can be used with many different cryptographically secure pseudo random function (PRF) I propose the widely spread HMAC algorithm here which we already know well from the last part of the series.
Like in the example above with the chained plain SHA-256 hash, the output of an HMAC operation is used as the input of the next HMAC operation. But now we seed each HMAC operation with the original password to protect from convergences concerning the password.
The salt is only used in the input of the first HMAC operation, but other than with simple chaining we also take the output of each HMAC operation and xor everything together to get the final output, so all bits of the first operations result (long before the value might be degraded) will have a direct influence on all bits of the final result. (See the graphics below.)
The RFC calls this technique of combining output/input chaining with xoring together all intermediate results a “belt-and-suspenders approach” The chaining forces an attacker to execute all HMAC operations sequentially while the xoring prevents any degeneration of the output values due to the repeated hashing.
Since the main use of PBKDF2 besides password hashing is the generation of “key material” from a user supplied password, the algorithm also introduces a block counter to allow the generation of any number of cryptographic keys of arbitrary sizes from a single password.
Putting it all together, the PBKDF2 algorithm looks like this:
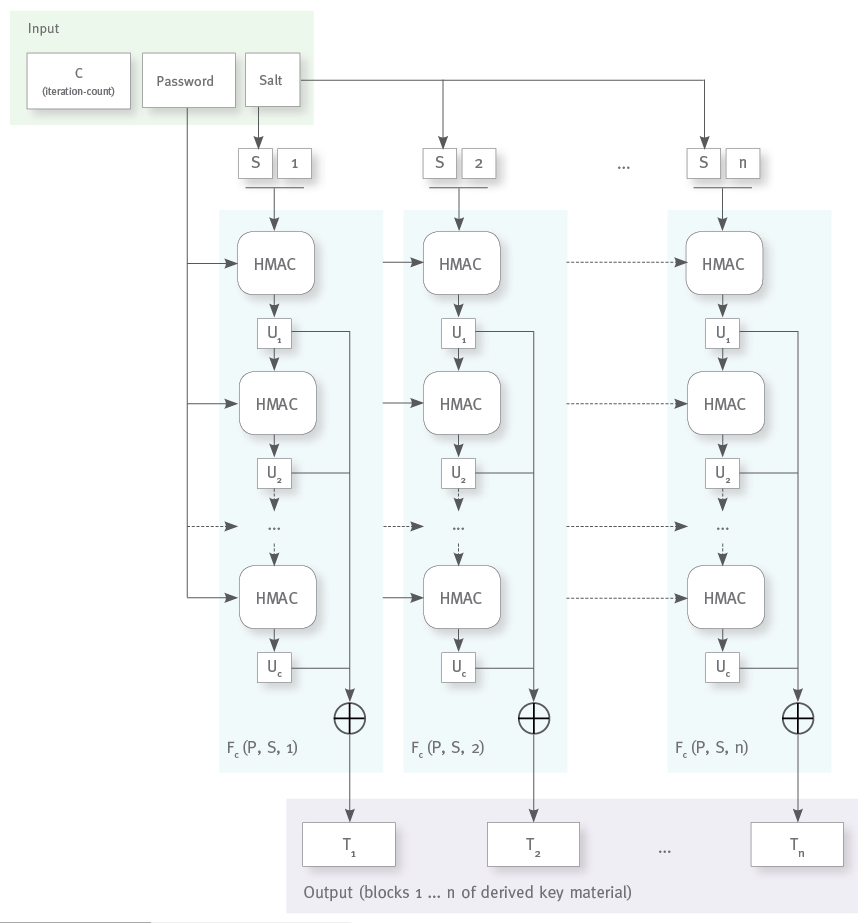
At the core of the algorithm lies the Fc(P, S, i) function which generates a single block of “key material” from the password P, the salt S, the block index i and the iteration count c; it implements the chained application of the HMAC operation and the xoring of the intermediate results.
For pasword hashing you will normally not need to calculate multiple output blocks. The 256 bits of output you get from HMACSHA-256 is plenty for a password hash value (not to speak of HMACSHA-512), so you can reduce the PBKDF2 algorithm to the calculation of Fc(P, S, 1) and take its output (truncated to 256 bit if necessary) as the value of your password hash.
Is it Worth the Pain?
That is a very good question. If you find PBKDF2 in your crypto library ready to use, then the answer is most probably “yes”. But you should not expect any miracles. When choosing the iteration count, you will be limited by the performance of your target machines. No user will tolerate to wait for minutes or even hours when trying to log into a system. And the typical crypto library used in business applications and the hardware executing your applications will not be optimized for high performance hashing.
The attacker on the other side is practically only limited by the price he is willing to pay to crack the passwords. Dictionary attacks on hashed passwords are perfectly parallelizable. Just split the dictionary into as many fragments as you have processing units at hand. The more processing power you can throw at the problem the faster you will get a “solution”.
I already mentioned that a modern GPU can easily beat a server CPU by a factor of 200 when doing parallel hashing operations. An attacker could further improve his chances by upgrading his PC with multiple GPUs. And then maybe buy a second PC with a few GPUs and a third. But nowadays you don’t really need to invest in hardware yourself. Just rent as much computing power as you like (and can afford) from some cloud service.
Even more dangerous to hashed passwords is modern hardware like ASICs which is what contemporary Bitcoin miners use for their trade. Since these people actually make money from calculating hashes as fast and cheap as possible (which is all that Bitcoin mining is about), it is very likely that the specialiced hardware most popular with them will also be the optimal choice for cracking password hashes.
Well, for the present time (but probably not for very long) there is still a defense against highly specialized ASICs. The final part of this series will take a closer look on the scrypt algorithm which is designed to provide at least some protection against precisely such hardware.
